Если в бочку дегтя положить ложку меда, получится бочка дегтя. Если в бочку меда положить ложку дегтя, то получится бочка дегтя. Если положить ложку дегтя в бочку дегтя, получится бочка меда. Если вы положите ложку меда в бочку меда, то получите бочку меда.
Сложение и вычитание отрицательных и положительных чисел — правило, формулы и примеры
Отрицательные числа впервые вводятся в 6 классе, иногда раньше. Число со знаком «+» называется положительным, а противоположное число — отрицательным.
Чтобы понять сложение и вычитание положительных и отрицательных чисел, просто используйте координатную линию. Пример: сумма чисел равн а-18 и 2. Используя координатную линию, отметьте число (-18), затем добавьте 2 единичные дроби с правой стороны линии, и координатная линия покажет сумм у-16.
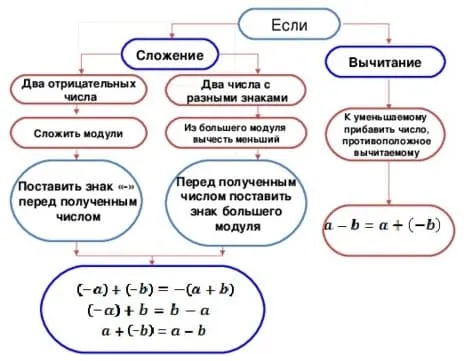
Правило сложения отрицательных чисел и чисел с разными знаками
Чтобы сложить два отрицательных числа, нужно сложить два отрицательных числа:
- суммировать их модули;
- перед полученной суммой поставить знак «минус».
Например, если сложить числ а-9 и-6, то это будет выглядеть следующим образом:
В этом случае вы складываете модули 9 и 6 и ставите символ «-» перед получившимся натуральным числом 15.
Рациональные или дробные числа складываются таким же образом:
-26,35 + (-25,35) = -(26,35 + 25,35) = -51,75
Мы прибавляем 25,35 к 26,35 (т.е. складываем модули) и получаем 51,75 с отрицательным значением. Поставьте перед ним знак минус.
Чтобы сложить натуральные числа со знаками «+» и «-«, нужно:
- из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
- перед полученным результатом поставить знак того слагаемого, которое имело большее значение.
61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
Квадрат большего числа со знаком «+», поэтому сумма положительна:
-81 + 35 = -(81 — 35) = 46
Большее число имеет знак «-«, поэтому замените плюс на минус и получите отрицательный ответ.
Как вычитать отрицательные и положительные числа
Чтобы найти разность противоположных чисел, прибавьте к вычитаемому вычитаемое с противоположным знаком, т.е. замените разность суммой.
Этот процесс лучше всего иллюстрируется формулой:
То есть, каждое выражение со знаками сложения и вычитания должно быть решено как сумма чисел.
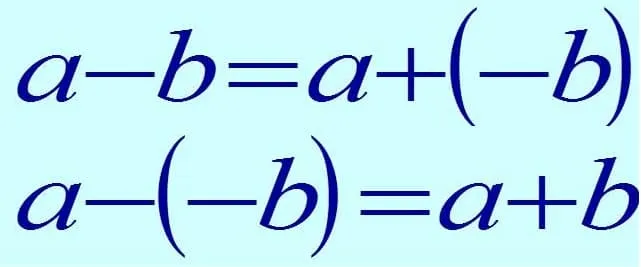
-20 — 14 = -20 + (-14) = -34;
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения положительна, если уменьшающий коэффициент больше вычитающего, и отрицательна, если значение уменьшающего коэффициента меньше вычитающего. Если вычитаемое и вычитатель одинаковы, то разность равна нулю.
- 15 — 6 = 15 + (-6) = 9 — уменьшаемое 15, больше вычитаемого, поэтому ответ положительный;
- -15 — 6 = -15 + (-6) = -21 — уменьшаемое -15, меньше вычитаемого, следовательно, ответ отрицательный.
Если нужно вычесть отрицательное число, то два последовательных знака минус дают знак плюс.
10 — (-5) = 10 + 5 = 15;
— 10 — (-5) = -10 + 5 = 5 — 10 = -5.
Все вышеперечисленные операции можно выполнить с помощью калькулятора. Для этого просто введите сначала коэффициент числа, а затем нажмите клавишу смены знака.
Например, чтобы установить числ о-81,73, нажмите клавиши в следующем порядке: «8», «1», «,», «7». «3», «+/-«. Чтобы решить пример с отрицательными числами, действуйте в том же порядке, что и с положительными числами.
Правила знаков

В математике минус и плюс — это символы для обозначения отрицательных и положительных чисел. Они по-разному взаимодействуют друг с другом, поэтому необходимо соблюдать правила знаков при любых операциях с числами, таких как деление, умножение, вычитание, сложение и т.д. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Не зная этих правил, можно изучать не только математику, но и физику, химию, биологию и даже географию.
Давайте подробнее рассмотрим основные правила знаков.
Деление.
Если мы делим плюс на минус, то всегда получаем минус. Если мы делим «минус» на «плюс», то всегда получаем «минус». Если мы разделим плюс на плюс, то получим плюс. Если мы разделим «минус» на «минус», то парадоксальным образом получим «плюс».
Если мы умножим минус на плюс, то всегда получим минус. Если мы умножим «плюс» на «минус», то всегда получим «минус». Если мы умножим «плюс» на «плюс», то получим положительное число, которое равно «плюс». То же самое относится и к двум отрицательным числам. Если мы умножим «минус» на «минус», то получим «плюс».
Вычитание и сложение.
Они основаны на другом принципе. Если отрицательное число больше нашего положительного числа, то результат, конечно же, отрицательный. Возможно, вам интересно, что такое модуль и зачем он вообще нужен. Все очень просто. Модуль — это значение числа, но без знака. Например, -7 и 3. По модул ю-7 — это просто 7, а 3 — это все еще 3. В результате мы видим, что 7 больше, поэтому наше отрицательное число больше. Таким образом, получае м-7+3 = -4. Можно сделать еще проще. Просто поставьте положительное число на первое место, и в результате получится 3-7 = -4. Может быть, кому-то так будет понятнее. Вычитание работает точно так же.
| Правила умножения (деления) чисел | ||
|---|---|---|
| Мультипликаторы | Результат | |
| Разделенный | Разделитель | |
| + | + | + |
| + | — | — |
| — | + | — |
| — | — | + |
Правило знаков
Эта тема часто связана с понятием правила точки, которое рассматривается на уроках математики в шестом классе. Стоит уточнить этот момент.
Правило знака фактически является производным от правил умножения отрицательных и положительных чисел. Например:
6-(-6)=6+(-1*-1*6)=6+6 — но это слишком долго, чтобы повторять каждый раз, поэтому проще один раз запомнить, что умножение минуса на минус и плюса на плюс дает знак плюс. А умножение «плюса» на «минус» дает «минус». Эти правила легко запомнить, поэтому вам не придется беспокоиться о том, чтобы каждый раз получать множественные числа.
Сложение и вычитание отрицательных чисел
Давайте рассмотрим каждый процесс отдельно, чтобы не возникало лишних вопросов.
Сложение отрицательных чисел
Добавление может осуществляться между:
Вычитание отрицательных чисел
Вычитание может быть выполнено между:
- Двумя отрицательными числами. В этом случае «”минус” на “минус”» дает “плюс”. После этого, мы увидим выражение из предыдущего пункта, то есть сложение отрицательного числа с положительным. Нужно поменять числа местами и выполнить вычитание.
- Отрицательным и положительным числом. В этом случае получается та же ситуация, что при сложении двух отрицательных чисел. Так как, “минус” на “плюс” дает “минус”. Получившиеся числа складываются по модулю, а потом к результату возвращают “минус”.
- Положительным и отрицательным числом. Этот случай больше прочих любим составителями примеров. В результате преобразования по правилу знаков: «”минус” на “минус”» дает “плюс”. Значит, получится сложение двух положительных чисел.
Следует добавить, что прибавление или вычитание нуля не влияет на отрицательное число. Однако вычитание числа из нуля меняет его знак на противоположный.
Математика для блондинок
Математикой должны заниматься блондинки — они не умеют лгать.
Минус на плюс что дает?
Математики изобрели положительные и отрицательные числа. Им нечем было заняться, и они придумали это. Те же математики придумали правила умножения и деления положительных и отрицательных чисел. Просто чтобы облегчить нам жизнь. Что мы должны делать? Нам нужно выучить правила, чтобы мы могли сказать математикам, чего они от нас хотят.
Правила умножения и деления положительных и отрицательных чисел легко запомнить. Если два числа имеют разные знаки, результатом всегда будет минус. Если два числа имеют одинаковый знак, результатом всегда будет плюс.
Давайте рассмотрим все возможности. Что превращает минус в плюс? При умножении и делении минус на плюс дает минус. Что делает из минуса плюс? Когда мы умножаем и делим, результатом также является минус.
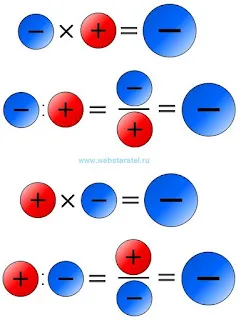 |
| Минус на плюс, плюс на минус. |
Как видите, все возможности умножения и деления положительных и отрицательных чисел исчерпаны, но у нас по-прежнему нет знака плюс. Мы создали это правило для себя, чтобы помнить о нем. Что мы скажем математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.
Что дает минус за минус? Когда мы умножаем или делим, всегда есть плюс. Что дает плюс за плюс? Здесь все очень просто. Умножение или деление плюса на плюс всегда дает плюс.
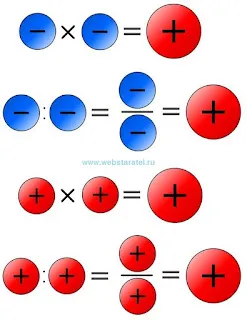 |
| Минус на минус, плюс на плюс. |
Надеюсь, вы помните: минус на минус дает плюс, плюс на плюс дает минус. Что скажут математики? Когда вы умножаете и делите положительные или отрицательные числа, результатом будет положительное число.
Если при умножении и делении двух плюсовых чисел все понятно (результат — тот же плюс), то при умножении и делении двух минусовых чисел ничего не понятно. Если два плюса дают плюс, то два минуса, по логике, должны давать минус. Такой большой, жирный минус. Но такого не существует. Математики смотрят на это по-другому. Так почему же минусы становятся плюсами?
Уверяю вас, математики интуитивно решили проблему правильного умножения и деления плюса и минуса. Они написали правила в учебниках, не вдаваясь в излишние подробности. Чтобы правильно ответить на вопрос, нужно понять, что означают знаки плюс и минус в математике.











